일본에서 일하면서 회사 테크블로그에 글을 게시하고 있습니다.
부족한 일본어지만, 이전에 제 블로그에 투고한 글들을 정리하고
관련테마로 새롭게 조사한 내용도 있기에 번역기로 살펴보시면 좋을것 같습니다.
「目次」
- 科学書との因縁
- 素数の足跡
- 素数とRSA暗号化
- 量子コンピューターとRSAの未来
1.科学書との因縁
こんにちは、ジーマックスメディアソリューションのLimです。
私が初めて運用した個人ブログは自然にTechBlogのようになりました。
ブログ運営の長所は自分が知っていると思った知識も他の人々に説明する時には
ところどころに穴があって自分が逃していた知識を手に入れて
より固くその知識をまとめられることでした。
ブログを開始した時は大学の頃ですのでほとんどの投稿は専攻である
コンピューターに関したことでしたが共に私の好みだった科学書のことごともありました。
私は高校生3年ずっと図書部でした。実際に思う存分本を読めるサークルは読書部で、
図書部はギリシャ神殿デザインのかなり大きな図書館を毎日掃除したり
昼ご飯の時間にもシフトで学生たちが返却する本を整理したりしました。
その代価はどのサークルよりも溢れる奉仕活動点数でした。私も最初は奉仕点数のため
入部しましたが段々図書館の本に書かれた数字と文字、そしてバンドの色で
学生たちが求める本を早く探してあげることが面白くてやりがいがありました。
そしてあの日、本を整理しながら本当に面白そう本が目に入りました。
「超ひも理論と隠された次元、そして究極の理論に向けた探求旅行」
ブライアン・グリーンさんのエレガント・ユニバスという科学書でした。
今も覚えています。私はただその厚い本が退屈な毎日に逃げ場ように見られました。
ところでその本はその日常よりも退屈なものでした。最初は本の流れはどころか
10ページも読む前に眠りを堪え難かったです。本にはニュートンなどの古典物理学から
最近の宇宙を説明する2つの物理理論が説明されてありました。相対性理論、そして量子力学を
説明したあと著者自分が研究している超ひも理論がその2つの理論を繋げる統一理論だというのが
その本の主な流れでした。まるで紙で作った天然睡眠薬見たいな内容ですね。
ところでブログ運営と図書部サークル活動が思ったこととは違う利点があったように
そのような科学書を読む習慣がくれた考え方は何よりも私のこころの根底に根付きました。
第一に、難しさの基準が変わりました。その前は課題などで困った時に、
「なぜ私がこのような退屈なものに心を掴まれているのだろう。面白いゲームがしたい」
と感じられました。ところでこの世界で(私の思いでは)人間として本当に難しい、
何よりも意味あることごとを今も解決している科学者たちがいることを思って不平より
私にできることを一つ一つやって行く心得になりました。
第二に、知識を吸収する方式を見つけました。最初厚い本を読む時にはほぼ600ページに中で
私が理解した内容は30ページもできませんでした。ところで著者の他の本を読んだり
より絵が多いニュートン見たいな科学雑誌を読んだりしたら私がただ文字列として覚えていた
本たちのそれぞれの断片が自然に繋がりました。難しい内容を早く理解することはできなくても
どんな難しいことも色んな本または反復で理解できることを確信しました。
コンピューターは科学の立派な結果物です。ところで科学書そのものの情報が科学者ではない
私の生に役に立った経験は少ないです。まるで料理人が食べ物のために肥料の成分と歴史を
知らなくても相変わらず美味しい食べ物を作るように。ところでそれはありそうなことです。
ただ私が初心の料理人のためかも..
幸いにここでお伝えたい内容はその中でも科学書と連関性があることです。
2.素数の足跡
皆さん、もしかして素数(Prime Number)にご興味ありますか。
「1とその数以外の自然数では割らない数」です。
3と11見たいな数はすぐに素数だと分かります。
でも31,448,696,501見たいな数はメモ帳があっても早めに素数だと分かりにくいです。
小学生の時に数学教科書でしばらく挨拶したあと時々合われる友達です。
ところでこの子は私を友達だと思えないかも知れません。
なぜならばこの子は私より年齢がはるかに上です。
素数の規則性を求める研究は2,300年前のユークリッドの著書、’原論’でもありました。
ユークリッドは紀元前時代で、素数の無限性を証明しました。以下のように。
AとBが今我々が知っている素数だと仮定しましょう。
そしてAとBを掛け合せると新しい数のCになります。
それじゃ「C+1」はAとB、どの数でも割っても1が残りますね。
これから2つの場合があります。第一はその「C+1 (= A*B+1)」が新しい素数の場合、
第二はAとBもない新しい素数で割られる場合です。どんな場合も新しい素数の誕生です。
その中を知れないものが終わりも知らないですね。
そのドラゴンボールのフリーザーさんもただ3段変身まででしたが素数は無限にそのあとがあります。
ユークリッドが亡くなった10年後に生まれたエラトステネスは「エラトステネスのふるい」という
素数判別方法を見つけました。太陽による影の差異で地球の周りを計算したことでも有名な方です。
エラトステネスのふるいは並んでいる数の中で見つけた素数の倍数は素数がないという簡単な方式で
素数を判別します。素数の定義をそのまま適用した見たいなことです。ところでこれが今日まで
コンピューターなどで素数を検証する一番確確かな方法です。
1792年、ドイツの数学者であるガウスが意味深い発見をしました。ただ概算ですけど
以下のような公式で素数の図体を計れます。これがガウスの素数定理です。
分母は対数関数で素数の頻度が対数関数に反比例してあります。
ガウスは15歳のごろ、手で毎日1000個ずつの素数を探しながらこのような素数定理を発見しました。私がそのごろ一日で10000匹ほど狩ったモンスターたちは全然役に立たなかったですが..
またこのようなこともあります。ニュートン雑誌で見たフリヒタの素数の十字架です。
自然数を24個ずつ以下のように羅列すれば2と3を除いて全ての素数が十字路に現れるます。
かなり不思議ですが、実はこれはただのごまかしでした。それを私も今更分かりました。
雑誌にはそのごまかしまでは説明できませんでした。今あのブログでこのような十字架ができるべきの理由を見つけました。やはりブログ書き物は知識の穴を埋めますね。
素数が現れない部分は偶数、そして余りなどの規則性のためでした。
「この素数の十字架に対して規則性を説明したサイトのリンクです。」
「プリヒタの素数円」は当然の結果です from azui
3.素数とRSA暗号化
ミステリーな素数に比べて人の成果はまだ少ないです。まるで素数は宇宙に掛かった錠の見たいな
ことですね。ところで人は逆にその錠を盗んでインタネット世界を支う暗号化方法として使っています。素数のミステリーを使った暗号化方式はRSAと言われます。
その暗号化方式を発明した3人の名字の頭文字で作名されました。
それじゃRSA暗号化を使って見ましょう。
ここでは私が皆さんのコンピューターにRSA暗号化としてデータを送る状況を仮定します。
私はあなたに「8」を送りたいです。
RSAは暗号化に公開キー、復号化には公開キーと秘密キーを使います。
公開キーは全ての人々が知っています。
ところで秘密キーは自分だけが自分のことを知っています。
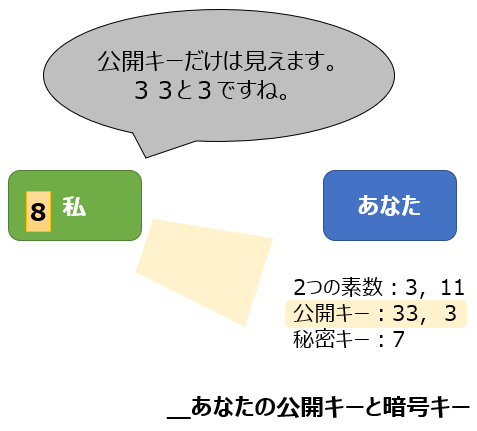
公開キーは2つの数です。第一はあなたが持っている2つの素数、3と11と仮定すれば
この2つを掛けた「33」です。そして各素数から1を引いたあと掛けた20,
それより小さな素数を一つ選びます。ここでは第二の公開キーとして「3」を選びます。
秘密キーはこの3に掛けたあと20として分けば余りが1にならなければなりません。
それゆえ秘密キーは「7」ですね(3 * x = 21)。
それであなたの公開キーは(33, 3)として、秘密キーは7として決定されました。
公開キーは私と、私とあなたのメッセージを盗み見たい悪い人を含めて全ての人々が知っています。
暗号化は本当に簡単です。
私があなたに送りたいデータは8でした。私は送りたい「8」をあなたの第二公開キーである
3として自乗します。そして第一の公開キーである33として割ってその余りを求めると
暗号化完了です。17ですね。暗号化は誰も楽にできます。
それじゃ復号化の番ですね。ここで素数の不思議な力が発揮されます。私が送った暗号化データを
あなただけが知っている秘密キーの7として自乗して第一の公開キー33として割って
その余りを求めると原本のデータの8になります。
皆さんもお感じられたようにRSA暗号化は材料であるその素数が大きければ大きいほどいいです。
33見たいな小さな公開キーはただ目で見ても3と11の素因数で分解されます。
それじゃ第二の公開キー3と、3と11としてできる20として秘密キーが7ということが
すぐにばれます。
4391と8819は2つとも素数です。この2つを掛け合せば38724229になります。
ところで38724229を初めて見た人はこれが4391と8819として割られることを
コンピューターなしで知ることはかなり難しいですね。それがRSAの力です。
4.量子コンピューターとRSAの未来
今日のディジタルコンピューターはメモリの蓄電器に電気を詰めたり空けたりして
0と1のデータを処理しますね。ところで今研究中の量子コンピューターというものは
蓄電器のディジタルビットではなくて原子を論理演算に活用します。
これはRSA暗号化に新しい危機になうそうです。既存のディジタルコンピューターは
エラトステネスのふるいのような方式でそのコンピューターの性能向上が
RSAの秘密キーを探すポイントでした。ディジタルコンピューターの性能向上は
普通マルチコアとしての並列性ですね。ところで量子コンピューターの並列性はそれと違います。
ディジタルコンピューターの並列性は別途のCPUコアが作業を「分担」しますが、
量子コンピューターのQubit(Quantum bit)は量子重畳という現象でビットである原子たちが
物理的に繋がってあります。この量子コンピューターの量子重畳がRSA暗号化の危機になります。
量子コンピューターの重要な応用分野になったピーター・ショアのショアアルゴリズムは
量子的な重畳現象でRSA暗号化を解体させることを見せました。以下のようなメカニズムです。
- 1.公開キー33より小さな数を任意で一つ選びます。私は5を選びました。
- 2.選択した5を自乗しながら33で割ったあと余りを求めます。
3.10を周期で繰り返されることを知れます。
探した周期の折半である5を初めて選んだ5として自乗します。3125です。
4.3125の上下で±1した数、3124, 3126と33との最大公約数を求めると3124とは
11, 3126とは3ができます。33の素因数である3と11を求めました。
これで秘密キー7も求めます。
ここで一番煩わしい部分は5を自乗しながら10という反復周期を探す部分です。
ディジタルコンピューターはこの部分で利点がありませんが、量子コンピューターは
量子間の絡みで重畳された10という周期が観測されるそうです。25か31見たいな特定の数ではなく
周期だけを観測するためフーリエ変換が適用されるそうです。
RSA暗号化のため我々はインタネット世界を安全に使用できます。お金が入っているかばんを持って
外国に直接行かなくても外国の物件がECサイトで決済されます。その他にも会社の重要な情報も
RSA暗号化されてインタネットで流れてあります。そのため今インタネットサービスを提供する
一部の通信社は量子コンピューターに対しても信じられる量子暗号化製品を開発しているようです。
読んでくださってありがとうございます。






댓글 없음:
댓글 쓰기